Bachelorthesis

Implementation of a Modular Camera Calibration Application in Mathematica

Sabine Schleise
Hochschule Furtwangen

Abstract

This thesis addresses the development of a modular application for computing camera calibration using the computer algebra system Mathematica. The work begins with a theoretical foundation in central projection and projective geometry, followed by the mathematical background of camera calibration. The calibration is based on the Image of the Absolute Conic (IAC) approach, following Hartley and Zisserman. Synthetic chessboard patterns and their projections were generated, calibration algorithms were developed, and the 3D structure was reconstructed. Robustness was evaluated through simulated perturbations, and a bundle adjustment was applied using the Levenberg-Marquardt algorithm. Additionally, the feasibility of porting the computations to Python was explored.

Introduction

Camera calibration is essential for precise 3D reconstruction, photogrammetry, and computer vision applications. It involves determining both intrinsic and extrinsic parameters of a camera. This work implements a complete calibration workflow using synthetic data within Mathematica, emphasizing modular design for future extensibility.

Objective

The primary objective is to develop modular algorithms in Mathematica that calculate camera calibration parameters based on three synthetic images of a chessboard using the Image of the Absolute Conic. Following the calibration, a reconstruction of the chessboard is performed. The algorithms' robustness is tested under disturbances, and a Levenberg-Marquardt optimization minimizes reconstruction errors. Furthermore, the transferability of the calculations to Python is assessed.

Approach

Review of projective geometry and central projection fundamentals
Implementation of synthetic chessboard generation and projection onto the image plane
Calculation of intrinsic parameters using homographies and the Image of the Absolute Conic
Initial 3D reconstruction of object points from 2D projections
Simulation of perturbations to analyze calibration robustness
Optimization through bundle adjustment using the Levenberg-Marquardt algorithm
Partial attempt to port the workflow into Python

Implementation

The application is built modularly in Mathematica, allowing independent testing and extension of each component. Important numerical methods like singular value decomposition (SVD) and Cholesky decomposition are employed. The synthetic generation of calibration patterns enabled precise ground truth comparisons. Basic functionality was additionally prototyped in Python to evaluate portability.

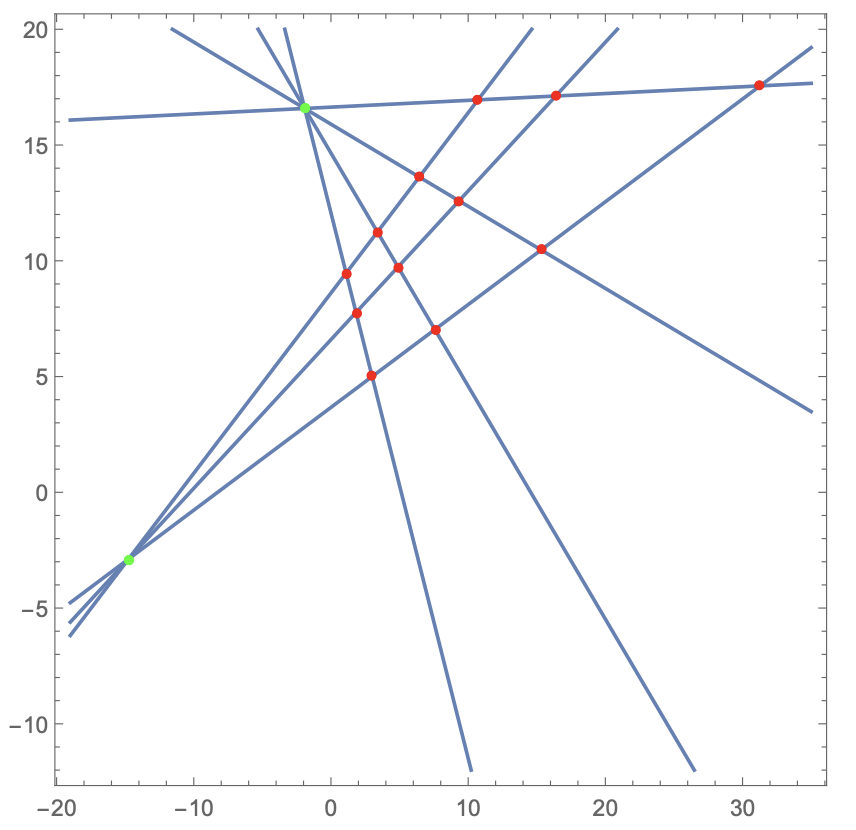
Example: Chessboard Projection and Vanishing Points

The following image shows a synthetic chessboard projection with detected vanishing points:

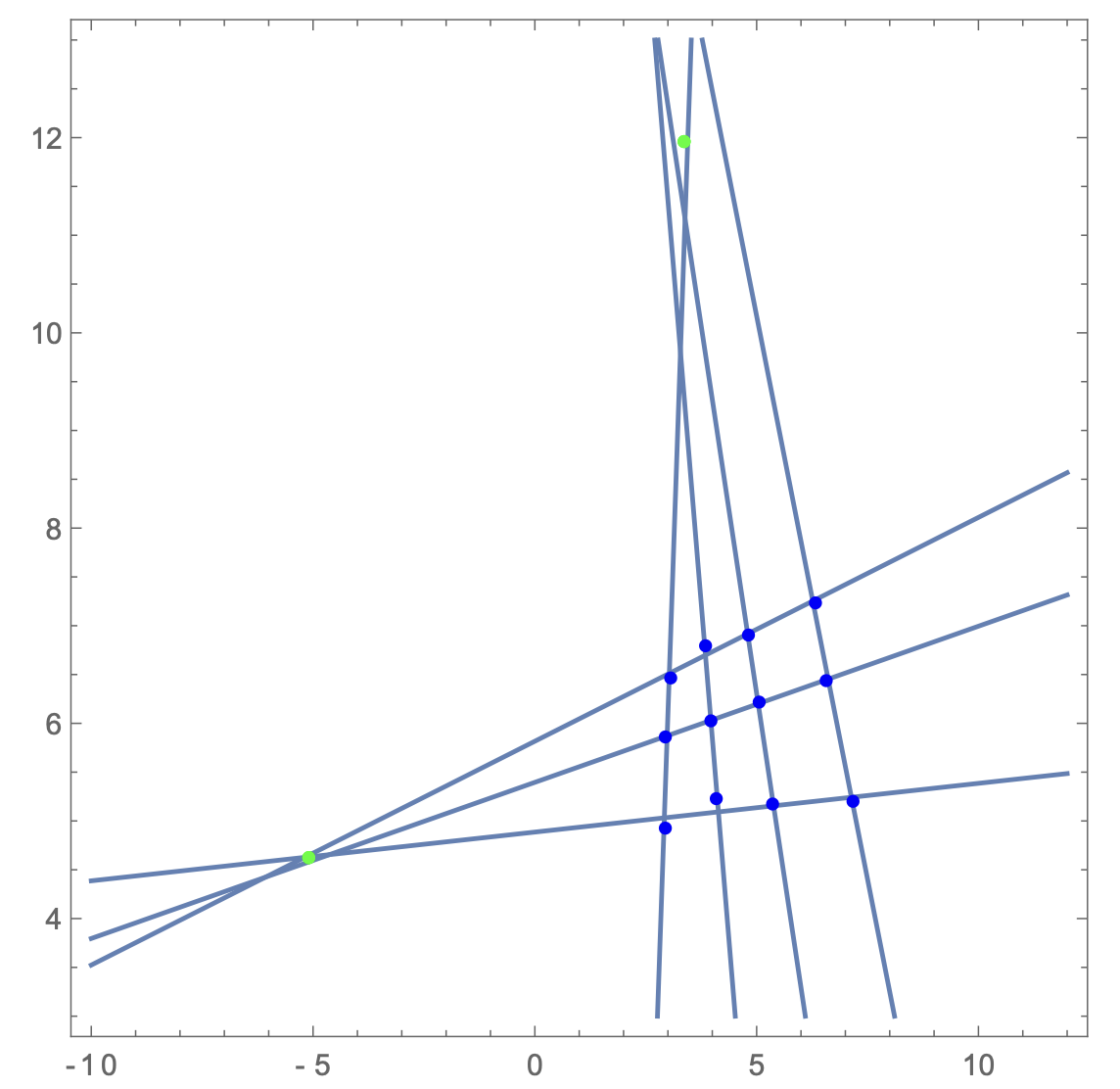
Example: Perturbation of Sensor Points

The next image demonstrates the perturbation of sensor points to test algorithm robustness:

Results

The calibration algorithms successfully computed the camera's intrinsic and extrinsic parameters from synthetic data. 3D reconstruction of chessboard points demonstrated high accuracy. Perturbations were introduced, and the robustness of the calibration was confirmed. Applying the Levenberg-Marquardt optimization significantly reduced reprojection errors. The porting to Python proved feasible but required careful handling of numerical precision.

Conclusion

This thesis shows that reliable camera calibration and 3D reconstruction can be achieved using synthetic data and advanced mathematical methods. The modular structure of the application facilitates future development toward a full standalone calibration tool. Optimization algorithms like Levenberg-Marquardt greatly enhance result quality, especially under realistic error conditions.

Supervisor: Prof. Dr. Thomas Schneider
Co-Supervisor: Prof. Dr. Ruxandra Lasowski
Date: February 28, 2022
Email: schleisesabine@gmail.com

*****